! Mean in Math: The Tiny Detail Students Always Miss

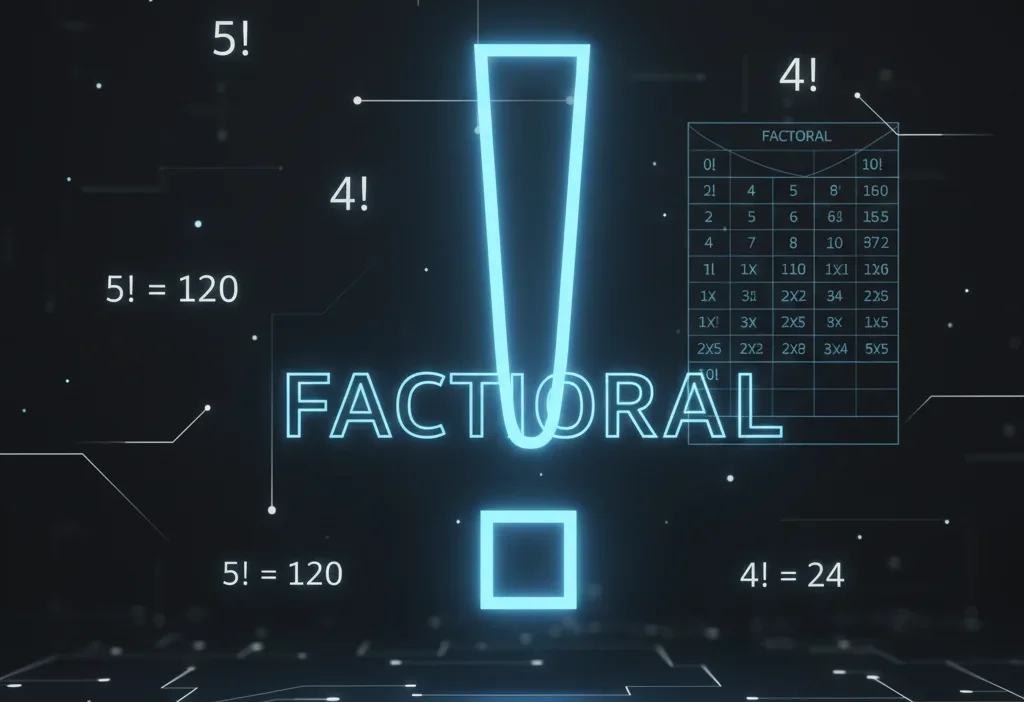
The first time I saw a number followed by an exclamation mark in math—like 5!—I honestly thought the teacher was excited about the number. Why is math yelling at me? 😅
Later, I realized “!” in math has nothing to do with emotions—it’s actually a powerful symbol called the factorial, used in probability, permutations, combinations, and many real-world calculations.

If you’ve also seen something like 3!, 10!, or 0! and wondered “What does the exclamation point mean in math?” — this guide explains everything in the simplest way.

“!” in math means factorial. It represents the product of all whole numbers from the given number down to 1.
Example: 5! = 5 × 4 × 3 × 2 × 1 = 120

---

🧠 What Does ! Mean in Math?

In mathematics, the symbol ! is called the factorial.
When placed after a number, it means:

👉 Multiply all whole numbers from that number down to 1.

Example:
4! = 4 × 3 × 2 × 1 = 24

Factorials grow very fast — even 10! is already 3,628,800.

In short:
“!” = Factorial = Multiply everything down to 1.

---

📘 Why Is Factorial (!) Used in Math?

The factorial shows up in many areas of mathematics, especially when dealing with arrangements and counting.

It is mainly used in:

• Permutations (arrangements of items)
• Combinations (selecting items)
• Probability
• Sequences & series
• Binomial theorem
• Computer science algorithms

Simply put:
Whenever you need to count how many ways something can happen, you will probably use !.

---

🔢 How to Calculate Factorial (!) Easily

Here’s the simple formula:

n! = n × (n−1) × (n−2) × … × 1

Examples:

• 3! = 3 × 2 × 1 = 6
• 6! = 6 × 5 × 4 × 3 × 2 × 1 = 720
• 1! = 1

The only special case:

0! = 1 (by definition)

Even though it looks strange, mathematicians define 0! as 1 to keep formulas consistent.

---

📱 Where Is the ! Symbol Commonly Used?

Here are the main places where the factorial symbol appears:

📊 Mathematics

• Probability
• Permutations
• Combinations
• Algebra

🎮 Computer Science

• Algorithms
• Recursion
• Complexity analysis

📐 Statistics

• Probability distributions
• Counting methods

🎲 Real Life

• Arranging people
• Seating plans
• Password combinations
• Lottery calculations

🔍 Formality:
Factorials are formal mathematical notation, not casual or slang.

Chin Acne Mean: Why This Spot Shows Up Again and Again

---

💬 Examples of ! (Factorial) in Action

Here are simple, everyday-style examples:

Example 1:
“How many ways can 4 books be arranged?”
→ 4! = 24 ways

Example 2:
“How many 3-letter passwords from A, B, C?”
→ 3! = 6 passwords

Example 3:
“How many ways can 5 friends sit in a row?”
→ 5! = 120 arrangements

Example 4:
“Find 7!”
→ 7! = 5040

Example 5:
“How many ways to pick winners in order?”
→ Use factorial in permutations.

---

🕓 : When to Use and When Not to Use the Factorial (!)

✅ When to Use “!”

• Counting arrangements
• Probability calculations
• Combinatorics problems
• Any question involving “ways,” “orders,” or “arrangements”

❌ When NOT to Use “!”

• Basic addition or subtraction
• Random multiplication
• Equations unrelated to arrangements
• Everyday arithmetic

---

📊 Comparison Table: When Factorial Makes Sense

Context	Example Phrase	Why It Works
Counting Arrangements	“How many orders for 5 items?”	Factorial counts arrangements
Probability	“How many combinations?”	Factorial is used in formulas
Seating Plans	“Arrange 4 people in a row.”	Order matters → use !
Normal Math	“Solve 3 + 4.”	No factorial needed
Basic Multiplication	“Find 6 × 8.”	Not a factorial problem

---

🔄 Similar Mathematical Symbols You Should Know

Here are alternatives used with factorial:

Symbol	Meaning	Use Case
n!	Factorial	Arrangements, probability
nPr	Permutation	Ordered selections
nCr	Combination	Unordered selections
^	Exponent	Powers
√	Square root	Roots of numbers
Σ	Summation	Add many terms
Π	Product	Multiply many terms

SSID Mean: A Simple Explanation That Finally Makes Sense

---

📘 Factorial Trick for Fast Calculation

Here’s a simple trick:

If you know 5! = 120, then:

• 6! = 6 × 120 = 720
• 7! = 7 × 720 = 5040
• 8! = 8 × 5040 = 40320

You can build higher factorials easily from lower ones.

---

🧮Real-Life Uses of Factorials

You might be surprised how often factorials appear in real life:

• Arranging guests at a wedding
• Creating unique passwords
• Shuffling a deck of cards
• Lottery combinations
• Scheduling tasks
• Computer simulations

Fun fact:
A deck of cards has 52! possible arrangements — a number larger than the number of atoms on Earth!

---

📏 Common Mistakes Students Make With ! Symbol

• Thinking “!” means exclamation, not multiplication
• Forgetting that 0! = 1
• Trying to multiply the number with 1 only (e.g., 5! = 5 × 1 ❌)
• Using factorial in normal algebraic equations
• Assuming factorial works on decimals (it doesn’t for beginners)

---

❓ FAQs About the ! Symbol in Math

1. What does “!” mean in math?

It means factorial, which multiplies all whole numbers down to 1.

2. What is 0!?

0! = 1, by definition.

3. Why does 5! grow so fast?

Factorials multiply many numbers, causing exponential-style growth.

4. Can factorials be used for decimals?

Not in basic math — advanced math uses the Gamma function for that.

5. What is the largest factorial we use?

In computing, factorials beyond 20! become extremely large.

---

📝 Conclusion

The “!” symbol in math is the factorial, a powerful tool used in counting, arrangements, probability, and computer science. From simple classroom problems to massive real-life calculations like card shuffling and password generation, factorials help us understand how many possible outcomes a given situation can have.

Once you understand that n! = multiply everything down to 1, the entire concept becomes easy and even fun. Whether you’re studying math, preparing for exams, or exploring probability, factorials will appear again and again—so now you’re fully ready for them!